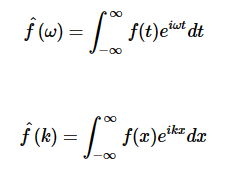The Fourier series is used to express a periodic signal as a combination of sinusoidal waves, meaning that we have a resultant signal that is made up of a combination of those sine waves. The Fourier transform is a formula that is used to transform a signal that was recorded in either time or space to the same signal sampled in the temporal or spatial frequency. Using this we can help find the frequency components of these signals. In real applications, signals can be muddied with noise which can hide their frequency components. The Fourier transform can process out that extra noise to reveal the frequencies thus making the Fourier series very good at filtering noise.
The Fourier Transform can either be f(t) for time or f(x) for time.
ω = angular frequency and is related to frequency
by
The units for frequency are usually in Hertz(Hz).
k = wavenumber, it has units of inverse length and is related to wavelength
by
References:
Washington, A. J., & Evans, R. (2017). Basic Technical Mathematics with Calculus (11th ed.). Pearson Education (US). https://ecpi.vitalsource.com/books/9780134507095
EngineerYourSound. 2023. What Is The Fourier Series Used For? (Real applications). What Is The Fourier Series Used For? (Real applications) – Loudspeaker & Acoustic Engineering Design (engineeryoursound.com)
Links to an external site.
Herman, Russell, 2022, LibreTexts Mathematics, 9.5: Properties of the Fourier Transform. 9.5: Properties of the Fourier Transform – Mathematics
